Mastering Graphing Vertex Form: A Comprehensive Worksheet Guide
Understanding Vertex Form
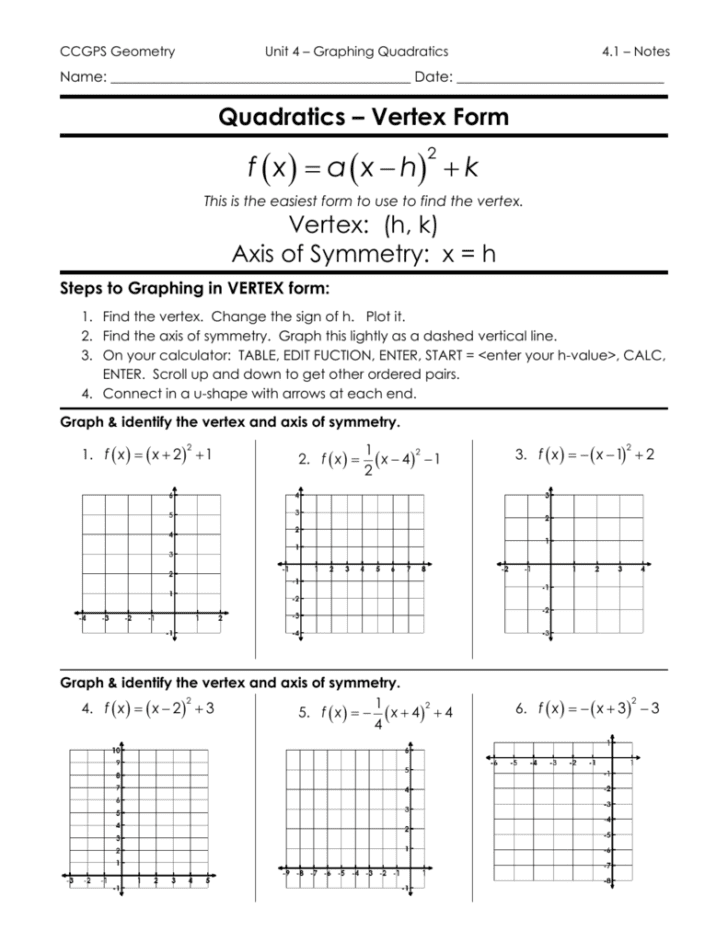
Graphing quadratic functions in vertex form is an essential skill for students of algebra and mathematics. The vertex form of a quadratic function is given by f(x) = a(x - h)^2 + k, where (h, k) represents the vertex of the parabola. Understanding how to graph these functions is crucial for visualizing and analyzing the behavior of quadratic equations. With a graphing vertex form worksheet, students can practice converting standard form quadratics to vertex form and vice versa, as well as identifying key features of the graph such as the vertex, axis of symmetry, and x-intercepts.
The process of graphing a quadratic function in vertex form involves several key steps. First, identify the vertex (h, k) from the equation f(x) = a(x - h)^2 + k. The vertex form makes it straightforward to find the vertex, as it is directly given by the values of h and k. Next, determine the direction the parabola opens based on the coefficient 'a'. If 'a' is positive, the parabola opens upwards; if 'a' is negative, it opens downwards. Finally, plot additional points to sketch the graph, using the axis of symmetry and the vertex as guides.
Practicing with a Graphing Vertex Form Worksheet
To effectively use a graphing vertex form worksheet, it's essential to have a solid grasp of the vertex form itself. This includes understanding how the values of 'a', 'h', and 'k' affect the shape and position of the parabola. The value of 'a' influences the width of the parabola and its direction, 'h' determines the x-coordinate of the vertex, and 'k' determines the y-coordinate of the vertex. By manipulating these values, students can see how changes in the equation affect the graph, enhancing their understanding of quadratic functions.
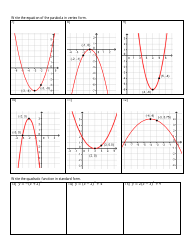
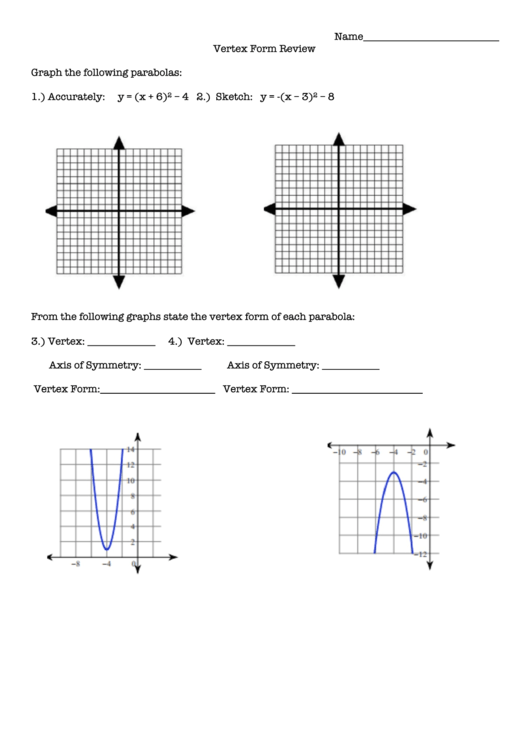
A graphing vertex form worksheet provides a structured approach to practicing and reinforcing the skills needed to graph quadratic functions in vertex form. These worksheets typically include a variety of exercises, such as converting between standard and vertex form, identifying vertices and axes of symmetry from equations, and graphing functions based on given vertices and other characteristics. By working through these exercises, students can build confidence and proficiency in graphing quadratic functions, preparing them for more advanced mathematical concepts and applications.